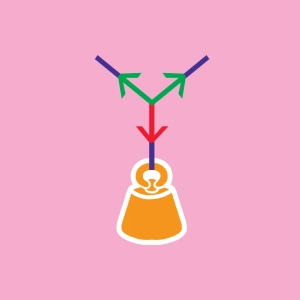
 Equilibrium of Three Forces
Equilibrium of Three Forces
A solid body submitted to three forces whose lines of action are not parallel is in equilibrium if the three following conditions apply :
- The lines of action are coplanar (in the same plane)
- The lines of action are convergent (they cross at the same point)
- The vector sum of these forces is equal to the zero vector.
In the animation, the forces are contained in the plane Pxy. P is the point of intersection and the vector sum of the forces is zero at all times. The mass is in equilibrium.
This state of equilibrium continues as long as the sum of the forces applied to the body remains zero. This corresponds to Newton’s Law of Inertia: “All bodies will maintain their state of rest or of uniform motion in a straight line that they are already in, unless acted upon by a force that would cause them to change their state of motion.”
The area of Mechanics that studies solids at rest is called Statics.
