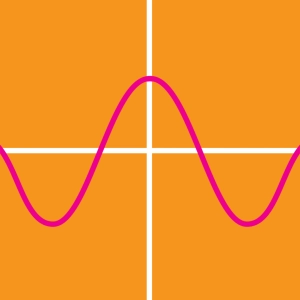
 Funciones seno y coseno
Funciones seno y coseno
Sea un punto ubicado en un círculo de radio A, cuyo centro coincide con el del sistema de coordenadas cartesianas. Este punto se identifica por su ángulo, denotado x (radianes).
La función seno representa la variación de la ordenada del punto en función de su ángulo x. La función seno tiene la ecuación f (x) = A sin (x).
La función coseno representa la variación de la abscisa del punto en función de su ángulo x. La función coseno tiene la ecuación f (x) = A cos (x).
Estas dos funciones tienen características comunes:
- Los valores de las funciones oscilan entre A y -A. El parámetro A corresponde a la amplitud de la función (la diferencia media entre el valor máximo y el valor mínimo).
- Un patrón (ciclo) se repite sin cesar: las funciones son periódicas con el período P: f (x + P) = f (x). La diferencia entre dos patrones se llama período, también es la diferencia entre dos máximos (o mínimos). Para la expresión básica, el período es 2π radianes (una vuelta completa del círculo): f (x + 2π) = f (x).
