 Función exponencial
Función exponencial
La función exponencial es una función de potencia donde la variable x es el exponente. En su forma básica, la función exponencial se escribe f(x) = qx o f(x) = expq(x).
El parámetro q es la base de la exponencial, es un real estrictamente positivo diferente de 1.
La variación de la función exponencial se estudia en dos intervalos:
- 0 < q <1: la función está disminuyendo estrictamente: f(x) → + ∞ cuando x → −∞ y f(x) → 0 cuando x → + ∞.
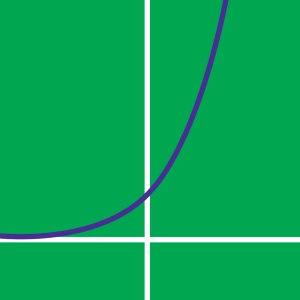
- q > 1: la función está aumentando estrictamente. f(x) → 0 cuando x → −∞. y f(x) → + ∞ cuando x → 0.
Si q = 1, entonces la función es constante. Es la línea de ecuación y = 1.
Si q ≠ 1, la función exponencial tiene para asíntota la línea de ecuación y = 0.
La función exponencial expq(x) es una función convexa que pasa a través del punto de coordenadas (0, 1): ∀ q, q0 = 1.
caso especial: La función exponencial que admite para la tangente al punto (0, 1) la línea de ecuación y = x, es la función exponencial básica e. Se denota f(x) = ex o f(x) = exp(x).
e es un número irracional, llamado número de Euler o número de Néper: e ≈ 2.718 281: e = f(1).
