Menu
🔎 🌎 FR ▾ Code classe 🔑 Connexion Abonnement
📂 ▾

Loi normale - Loi binomiale HTML5

Abonnement

Résumé

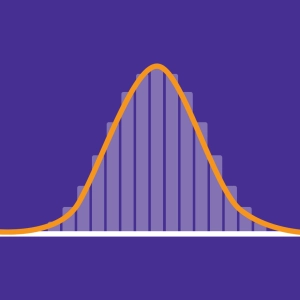
La loi normale décrit une distribution d'individus qui se répartissent symétriquement autour d'une moyenne. La majorité des individus se situe proche de cette moyenne, les autres s'en éloignent progressivement. Cette distribution normale forme une courbe en cloche aussi appelée courbe de Gauss.

De nombreuses grandeurs physiques approchent cette loi de distribution normale souvent décrite comme la loi des phénomènes naturels.  

Même si'il existe de nombreuses lois de probabilité, un phénomène issu du hasard, réitéré un grand nombre de fois, suit une loi de probabilité qui tend vers la loi normale. Ce théorème est illustré avec la loi binomiale.

Modifier les paramètres à l'aide des sliders. Cliquer puis faire glisser les limites a et b.

Objectifs d'apprentissage

  • Connaître la loi normale et l'influence de ses paramètres (moyenne et variance).
  • Connaître la loi binomiale et l'influence de ses paramètres (nombre d'épreuves n et paramètre de Bernouilli p).
  • Montrer que la loi binomiale se comporte comme la loi normale quand le nombre d'épreuves n augmente (Théorème de Moivre-Laplace).

En savoir plus

Une variable aléatoire Z suit une loi normale N(μ,σ2)si elle admet une densité de probabilité p(x) qui vérifie:

p(x) = 1/(σ√(2π)).exp( -(x-μ)2/(2σ2) )

μ représente la moyenne, σ l'écart type…

Abonnez-vous pour avoir accès à cette rubrique !