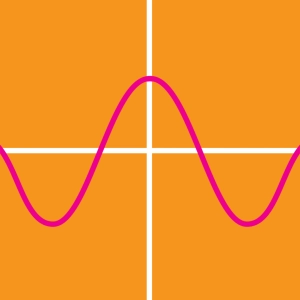
 Fonctions sinus et cosinus
Fonctions sinus et cosinus
Soit un point situé sur un cercle de rayon A, dont le centre coïncide avec celui du repère cartésien. Ce point est repéré par son angle, noté x (radians).
La fonction sinus représente la variation de l'ordonnée du point en fonction de son angle x. La fonction sinus a pour équation f(x) = A sin(x).
La fonction cosinus représente la variation de l'abscisse du point en fonction de son angle x. La fonction cosinus a pour équation f(x) = A cos(x).
Ces deux fonctions présentent des caractéristiques communes :
- Les valeurs des fonctions oscillent entre A et -A . Le paramètre A correspond à l’amplitude de la fonction (le demi-écart entre la valeur maximum et la valeur minimum).
- Un motif (cycle) se répète à l'infini : les fonctions sont périodiques de période P : f (x+P) = f(x). L'écart entre deux motifs s'appelle la période, c'est aussi l’écart entre deux maxima (ou minima). Pour l’expression de base, la période vaut 2π radians (un tour complet du cercle) : f(x+ 2π) = f(x).
