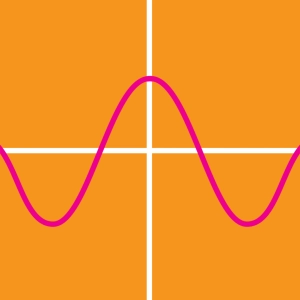
Sinus- en cosinusfunctie HTML5

Gegeven een punt gelegen op een cirkel met straal A, waarvan het middelpunt samenvalt met dat van een cartesisch assenstelsel. Dit punt wordt bepaald door zijn hoek, aangegeven met x (radialen).

De sinusfunctie representeert de verandering van de y-coördinaat als functie van de hoek x. De sinusfunctie heeft als voorschrift f(x) = Asin(x).

De cosinusfunctie representeert de verandering van de x-coördinaat als functie van de hoek x. De cosinusfunctie heeft als voorschrift f(x) = Acos(x).

Deze twee functies vertonen gemeenschappelijke kenmerken:

• De waarden van de functies oscilleren tussen A en -A. De parameter A correspondeert met de amplitude van de functie (de helft van het verschil tussen de maximale en minimale waarde).
• Een patroon (cyclus) herhaalt zich tot in het oneindige: de  functies zijn periodiek met periode P : f(x+P) = f(x). De afstand tussen twee patronen wordt de periode genoemd, dat is tevens de afstand tussen twee maxima (of minima). In de basisuitdrukking is de periode 2π radialen (een volledig doorlopen cirkel) : f(x+ 2π)  = f(x).