 Exponentiële functie
Exponentiële functie
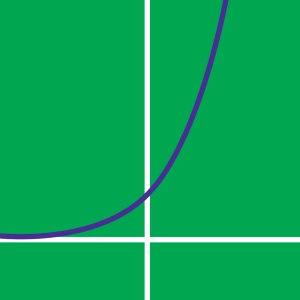
De exponentiële functie is een machtsfunctie waarvan de variabele x de exposant is. In de basisvorm wordt de functie geschreven als f(x) = qx of f(x) = expq(x). De paramètre q is het grondtal van de exponentiële functie, het is een strikt positief getal ongelijk aan 1.
De variatie van de exponentiële functie wordt bestudeerd op twee intervallen:
- 0 < q < 1: de fonctie is strikt dalend: f(x) → +∞ wanneer x → −∞ en f(x) → 0 wanneer x → +∞ .
- q > 1: de fonctie is strikt stijgend. f(x) → 0 wanneer x → −∞. en f(x) → +∞ wanneer x → 0.
Als q = 1 is de fonctie constant. Dit komt overeen met de rechte y = 1.
Als q ≠ 1 heeft de exponentiële functie als asymptoot de lijn y = 0.
De exponentiële functie expq(x) is een convexe functie die door het punt (0 , 1) gaat: q0 = 1.
bijzonder geval: de exponentiële functie die als raaklijn in het punt (0 , 1) de rechte y = x heeft, is de exponentiële functie met grondtal e. Deze wordt geschreven als f(x) = ex of f(x) = exp(x).
e is een irrationaal,getal dat het getal van Euler of het getal van Napier wordt genoemd: e ≈ 2,718281: e = f(1).
