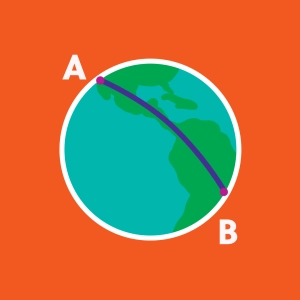
Orthodromie et loxodromie

On peut être surpris de voir, sur une carte, l'allure courbée des trajectoires empruntées par les vols long-courriers, ou les navires lors de grandes courses. Cela provient de la projection du globe terrestre (surface sphérique), sur une carte (surface plane). Cette projection induit nécessairement des déformations.
La projection de Mercator est souvent utilisée, car elle respecte les angles avec les méridiens. En revanche, elle ne respecte pas les surfaces : les régions polaires sont très fortement étirées horizontalement et verticalement (on ne peut d'ailleurs pas représenter les pôles, car ils sont rejetés à l'infini).
L'orthodromie est la route la plus courte sur le globe : c'est un arc de grand-cercle. Elle est représentée en rouge sur l'animation. Il n'y a que le long d'un méridien que sa représentation sur la carte de Mercator est un segment de droite. Pour suivre l'orthodromie, un navire doit constamment ajuster son cap.
Si un navire navique à cap constant, sa route est la loxodromie (en bleu sur l'animation). Elle forme une spirale qui s'enroule autour du globe. Toutefois, sur la carte de Mercator, elle est rectiligne, car la projection de Mercator conserve les angles.