 Normal distribution - Binomial distribution
Normal distribution - Binomial distribution
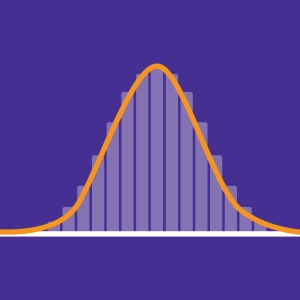
The normal distribution law describes a distribution of data which are arranged symmetrically around a mean. The majority of data is close to this average, others are moving away gradually. This forms a normal distribution bell curve also called Gaussian curve.
Many physical quantities approach this normal distribution often described as the law of natural phenomena.
Even though there are many laws of probability, a phenomenon born of chance, reiterated many times, follows a probability that tends towards the normal distribution. This theorem is illustrated with the binomial distribution.
Modify parameters with the help of the sliders. Click and drag the a and b limits.
