Normale verdeling - binomiale verdeling

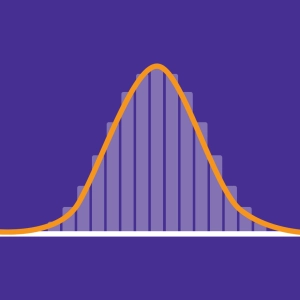
De normale verdeling beschrijft een verdeling waarbij de gegevens symmetrisch ten opzichte van een gemiddelde zijn verdeeld. Het merendeel van deze gegevens licht dicht bij het gemiddelde, en hoe verder van het gemiddelde hoe kleiner het aantal gegevens. ze vormen samen de klokkromme van de normale verdeling, ook wel gausskromme genoemd. 

Tal van fysische grootheden gedragen zich bij benadering volgens deze normale verdeling, vaak beschreven als de wet van de natuurverschijnselen. 

Hoewel er veel waarschijnlijkheidswetten zijn, volgt een toevalsverschijnsel dat vaak wordt herhaald een kansverdeling die nadert naar de normale verdeling. Een voorbeeld hiervan is de binomiale verdeling.

Verander de parameters met behulp van de schuifregelaars. Klik en versleep de a- en b-grenzen.